| |
| Lojra zbavitėse Lojra elektronike, Lojra tė ndryshme pa kufi. |
 18-05-07, 04:56
18-05-07, 04:56
|
#1
|
|
Illyria
Anėtarėsuar: 29-09-03
Vendndodhja: de
Postime: 44
|
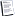 2+2=5
2+2=5
Tung lexues te nderuar dhe dashamire te matematikes
Egziston nje shembull matematikore, qe ne fund te te gjithave llogaritjeve plotesisht te sakta e fitojm relacionin 4 = 5 ose 2+2=5.
Kerkova mjaft ne kete forum, mendova se mos e ka postuar ndokush, por nuk e gjeta. Kerkoj ndjese ne qofte se gjindet e njejta teme ne forum.
Vertetimin e kam, por nuk e di se a munden te gjithe ta kuptojne. Duhet te i keni njohurite elementare te matematikes.
Urdheroni e provoni
Ndihme:
Nisuni prej -20=-20. Zberthene kete ekuacion. Duhet te perdorni katrorin e binomit.
Me rrespekt,
Maloku
__________________
Gabimet drjetskhrimore mbani per veti ... skeni nevoj ti diksutoni
|

|

|
 18-05-07, 08:43
18-05-07, 08:43
|
#2
|
|
Pickues
Anėtarėsuar: 20-03-07
Vendndodhja: Qaty ku o ngusht
Postime: 191
|
Zgjidhje logjike per 2+2=5 nuk ka.Kjo me teper njifet si sllogan i Stalinit per realizimin e planit 5 vjeqar per 4 vite.
|

|

|
 18-05-07, 10:58
18-05-07, 10:58
|
#3
|
Anėtarėsuar: 09-05-07
Postime: 151
|
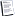
Siq tha edhe pleshti, nuk osh logjike qe 4=5, te pakten jo ne aritmetiken elementare. MIerpo ne shpesh keso forma te ngjashme i hasim gjat zgjidhjes se ekuacioneve te ndryshme, e ne ato raset kur na paraqiten forma te ngjashme psh si e jotja 4=5, apo 5=0, apo 3=6, perfundojm se ek nuk ka zgjidhje nga ajo bashkesi.
Per momentin jom ka muj me gjet veq nje menyre per me tregu ato qe e ke shkru ti 4=5, e per ma vone kur tkom kohe shohmi.
Nese e kemi nje ekuacion me vlera absolute te kesaj trajte:
Ix+1I-x+3=5,
Atehere ky ndahet ne dy intervale
1.nga minus infinit e deri te pika -1
2.si dhe nga pika -1 e deri te plus infinit.
ne rastin e pare ka zgjidhje, ndersa kur x merr vlera nga -1 e deri +infinit, ekuacioni i mesiperm e merr kete trajt:
Ix+1I=x+1, sepse x+1>0, prandaj kemi
x+1-x+3=4
x-at anulohen ktu edhe marrim 1+3=5 ose 4=5,, mirepo perfundimi ketu osht se ekuacioni nuk ka zgjiidhje kur x-i merr vlera nga (-1,+infinit).
Nderime,
P.s. do provoj edhe naj menyre tjeter per me ardhe ne rez. te ngjashme, mirepo me vone, se tani nuk po kame koh.
__________________
Be Good and You Will Be Lonely.
|

|

|
 18-05-07, 14:34
18-05-07, 14:34
|
#4
|
|
I pa pune
Anėtarėsuar: 16-02-04
Vendndodhja: Ne planetin Toke
Postime: 11,784
|
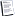
Citim:
|
Postimi origjinal ėshtė bėrė nga valmirii
Siq tha edhe pleshti, nuk osh logjike qe 4=5, te pakten jo ne aritmetiken elementare. MIerpo ne shpesh keso forma te ngjashme i hasim gjat zgjidhjes se ekuacioneve te ndryshme, e ne ato raset kur na paraqiten forma te ngjashme psh si e jotja 4=5, apo 5=0, apo 3=6, perfundojm se ek nuk ka zgjidhje nga ajo bashkesi.
Per momentin jom ka muj me gjet veq nje menyre per me tregu ato qe e ke shkru ti 4=5, e per ma vone kur tkom kohe shohmi.
Nese e kemi nje ekuacion me vlera absolute te kesaj trajte:
Ix+1I-x+3=5,
Atehere ky ndahet ne dy intervale
1.nga minus infinit e deri te pika -1
2.si dhe nga pika -1 e deri te plus infinit.
ne rastin e pare ka zgjidhje, ndersa kur x merr vlera nga -1 e deri +infinit, ekuacioni i mesiperm e merr kete trajt:
Ix+1I=x+1, sepse x+1>0, prandaj kemi
x+1-x+3=4
x-at anulohen ktu edhe marrim 1+3=5 ose 4=5,, mirepo perfundimi ketu osht se ekuacioni nuk ka zgjiidhje kur x-i merr vlera nga (-1,+infinit).
Nderime,
P.s. do provoj edhe naj menyre tjeter per me ardhe ne rez. te ngjashme, mirepo me vone, se tani nuk po kame koh.
|
(x+1)(-x+3)= -x+3x-x-3=-2x+3x-3=x-3
Kjo me poshte bene....
Ix+1I=x+1, sepse x+1>0, prandaj kemi
x+1-x+3=4
|

|

|
 20-05-07, 03:43
20-05-07, 03:43
|
#5
|
|
Thjeshtė ,njė zė!
Anėtarėsuar: 01-05-05
Vendndodhja: neutrale
Postime: 25,049
|
Kete ekuacion mund ta zgjidhin vetem shitesit !
__________________
Faleminderit qe ekziston !
|

|

|
 20-05-07, 03:47
20-05-07, 03:47
|
#6
|
|
I pa pune
Anėtarėsuar: 16-02-04
Vendndodhja: Ne planetin Toke
Postime: 11,784
|
Citim:
|
Postimi origjinal ėshtė bėrė nga vjeshta
Kete ekuacion mund ta zgjidhin vetem shitesit !
|
jo vetem ata por edhe atyre qe u pelqen matematika hihhihihih
|

|

|
 21-05-07, 10:56
21-05-07, 10:56
|
#7
|
Anėtarėsuar: 09-05-07
Postime: 151
|
Citim:
|
Postimi origjinal ėshtė bėrė nga giovanni
(x+1)(-x+3)= -x+3x-x-3=-2x+3x-3=x-3
Kjo me poshte bene....
Ix+1I=x+1, sepse x+1>0, prandaj kemi
x+1-x+3=4
|
Veq qetu jo "sepse x+1>0", mirepo "NESE" x+1>, ngase ne nuk e dim a osh ma e madhe se zero apo jo nese nuk tregojm se nga cili interval x-i merr vlera!!!!
__________________
Be Good and You Will Be Lonely.
|

|

|
 20-05-07, 05:28
20-05-07, 05:28
|
#8
|
|
Illyria
Anėtarėsuar: 29-09-03
Vendndodhja: de
Postime: 44
|
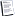
Citim:
|
Postimi origjinal ėshtė bėrė nga valmirii
Siq tha edhe pleshti, nuk osh logjike qe 4=5, te pakten jo ne aritmetiken elementare. MIerpo ne shpesh keso forma te ngjashme i hasim gjat zgjidhjes se ekuacioneve te ndryshme, e ne ato raset kur na paraqiten forma te ngjashme psh si e jotja 4=5, apo 5=0, apo 3=6, perfundojm se ek nuk ka zgjidhje nga ajo bashkesi.
Per momentin jom ka muj me gjet veq nje menyre per me tregu ato qe e ke shkru ti 4=5, e per ma vone kur tkom kohe shohmi.
Nese e kemi nje ekuacion me vlera absolute te kesaj trajte:
Ix+1I-x+3=5,
Atehere ky ndahet ne dy intervale
1.nga minus infinit e deri te pika -1
2.si dhe nga pika -1 e deri te plus infinit.
ne rastin e pare ka zgjidhje, ndersa kur x merr vlera nga -1 e deri +infinit, ekuacioni i mesiperm e merr kete trajt:
Ix+1I=x+1, sepse x+1>0, prandaj kemi
x+1-x+3=4
x-at anulohen ktu edhe marrim 1+3=5 ose 4=5,, mirepo perfundimi ketu osht se ekuacioni nuk ka zgjiidhje kur x-i merr vlera nga (-1,+infinit).
Nderime,
P.s. do provoj edhe naj menyre tjeter per me ardhe ne rez. te ngjashme, mirepo me vone, se tani nuk po kame koh.
|
I nderuari valmir
Dicka ke te drejte, por shume e ke komplikuar, matematicientet e mire nuk i nderlikojne kaq shume problemet, po mundohet ti dhjeshtesojne.
Ato in- apo ekuacione qe i perfitojme 0=a ato nuk kane zgjidhe, kane dmthnje tjeter, e jo qe a=0 apo pa marre parasysh 2 numra a=b. Keso gjarash hasim ne shume raste, por kjo nuk verteton kete problem.
Problemi eshte i thjeshte si ne vijim.

__________________
Gabimet drjetskhrimore mbani per veti ... skeni nevoj ti diksutoni
|

|

|
 21-05-07, 12:59
21-05-07, 12:59
|
#9
|
Anėtarėsuar: 24-12-06
Postime: 1,017
|
Citim:
|
Postimi origjinal ėshtė bėrė nga MaLoKu
I nderuari valmir
Dicka ke te drejte, por shume e ke komplikuar, matematicientet e mire nuk i nderlikojne kaq shume problemet, po mundohet ti dhjeshtesojne.
Ato in- apo ekuacione qe i perfitojme 0=a ato nuk kane zgjidhe, kane dmthnje tjeter, e jo qe a=0 apo pa marre parasysh 2 numra a=b. Keso gjarash hasim ne shume raste, por kjo nuk verteton kete problem.
Problemi eshte i thjeshte si ne vijim.
 |
Opa!
Deri tek "rrenjezimi" te dy anet e barazimit po jane te barabarta. Pastaj jo..
sepse 4 - 9/2 nuk eshte e barabarte me 5 - 9/2
(pra 8/2 - 9/2 = -1) (10/2 - 9/2 = 1)
Krejt cka po muj me kuptu ne kete sallate numrash eshte se paska raste ku rregulli, simbas te cilit barazimi nuk ndryshon, nese i pjeston/potencon/shumezon dy anet e tij me te njejtin numer, nuk po vlejka gjithmone. Dmth kur po rrenjezohen dy anet e barazimit, po prishet barazimi.. 
S“po di, por sidoqofte tani po e kuptoj me mire cka paska menduar mesuesja kur thojke: "Arton non calculat!!
Pershendetje!! 
|

|

|
 21-05-07, 18:23
21-05-07, 18:23
|
#10
|
Anėtarėsuar: 09-05-07
Postime: 151
|
PO arton ke shume te drejt kur thu se deri te rrenjezimi barazimi osht i sakt, pra ketu kemi gabim matematik, ngase eshte rregull matematikore qe kur e rrenjezojm a^ kjo nuk eshte e barabart me a por me vleren absolute te a-s per vet faktin se a mundet me qen edhe negative. prandaj aty ku rrenjezojm te problemi i malokut kemi (4-9/2)^2=(5-9/2)^2 kur te rrenjezojm ketu kjo matematikisht duhet shkruar keshtu
I 4-9/2 I=I 5-9/2 I
pra me vleren absolute te tyre, e jo vetem me to pa vlere absolute!!!!
Pra ekzistojn disa perkufizime ne matematike te cilat nuk na lejojne asnjehere per me ardh ne kontradikcione te tilla. ngase dihet logjikisht se nje gje e tille eshte e pamundur.
__________________
Be Good and You Will Be Lonely.
|

|

|
 18-05-07, 14:27
18-05-07, 14:27
|
#11
|
Anėtarėsuar: 24-12-06
Postime: 1,017
|
Citim:
|
Postimi origjinal ėshtė bėrė nga MaLoKu
Tung lexues te nderuar dhe dashamire te matematikes
Egziston nje shembull matematikore, qe ne fund te te gjithave llogaritjeve plotesisht te sakta e fitojm relacionin 4 = 5 ose 2+2=5.
Kerkova mjaft ne kete forum, mendova se mos e ka postuar ndokush, por nuk e gjeta. Kerkoj ndjese ne qofte se gjindet e njejta teme ne forum.
Vertetimin e kam, por nuk e di se a munden te gjithe ta kuptojne. Duhet te i keni njohurite elementare te matematikes.
Urdheroni e provoni
Ndihme:
Nisuni prej -20=-20. Zberthene kete ekuacion. Duhet te perdorni katrorin e binomit.
Me rrespekt,
Maloku
|
Krejt e lehte more!!
Duhesh vetem logaritmin e zeros ne katror mi potencu me njezetekatermbdhjete..
Ehhh kjo matematika.. Te ben me fole me gishta edhe sendet me te thjeshta nuk i kupton .. 
|

|

|
 20-05-07, 05:37
20-05-07, 05:37
|
#12
|
|
Illyria
Anėtarėsuar: 29-09-03
Vendndodhja: de
Postime: 44
|
Mos harroni e njejta gje vlen edhe per 3+3 =7 , 4+4 = 9 etj.
Keto quhen Sofizma matematikore (por sjam i sigurt se a quhet sakte keshtu) sa me kujtohen. (Termet shkencore po harrohen shpejt :S)
Mir'mbetshi
MaLoKu
__________________
Gabimet drjetskhrimore mbani per veti ... skeni nevoj ti diksutoni
|

|

|
 21-05-07, 19:22
21-05-07, 19:22
|
#13
|
Anėtarėsuar: 09-05-07
Postime: 151
|
Citim:
|
Postimi origjinal ėshtė bėrė nga MaLoKu
Egziston nje shembull matematikore, qe ne fund te te gjithave llogaritjeve plotesisht te sakta e fitojm relacionin 4 = 5 ose 2+2=5.
Maloku
|
Pra jo te gjitha llogaritjet jane plotesisht te sakta, i nderuar MaLoKu.
me respekt,
valmirii
__________________
Be Good and You Will Be Lonely.
|

|

|
 22-05-07, 19:55
22-05-07, 19:55
|
#14
|
Anėtarėsuar: 09-05-07
Postime: 151
|
Ja ma mire mos me shkru ma hiq une!!!!!!!!!!!!!!!!!
__________________
Be Good and You Will Be Lonely.
|

|

|
 23-05-07, 09:08
23-05-07, 09:08
|
#15
|
|
Illyria
Anėtarėsuar: 29-09-03
Vendndodhja: de
Postime: 44
|
Citim:
|
Postimi origjinal ėshtė bėrė nga valmirii
Ja ma mire mos me shkru ma hiq une!!!!!!!!!!!!!!!!!
|
Hahaha valmiri
Flm qe i ke shkruar tere keto postime. Ka edhe shume shume ... shume probleme matematikore qe japin rezultate te gabuara. Nuk di sa ke degjuar per nje program bankar, i cili ka shkaktuar miliona eurosh dem. Problemi ka qene pikerisht te llogaritjet. Per ate sduhet ti besohet matematikes e besa as kompjutorit ;).
Ku i ke permend vlerat absolute aty me larte. Nuk na ndihmojne, prap fitojme jobarazim edhe ne qofte se ato i leme. E ke vrejte edhe vet te inekuacionet e komplikuara, ne te shumten e rasteve nuk perfitojme zgjidhje te sakta.
Pamar parasysh
Rrespekt per ty, dhe per shenimet tua
MaLoKu
__________________
Gabimet drjetskhrimore mbani per veti ... skeni nevoj ti diksutoni
|

|

|
|
Anėtarėt aktiv qė janė duke parė kėtė Temė: 1 (0 Anėtarėt dhe 1 Guests)
|
|
|
 Rregullat E Postimit
Rregullat E Postimit
|
You may not post new threads
You may not post replies
You may not post attachments
You may not edit your posts
Kodi HTML ėshtė OFF
|
|
|

Hyrja | Chat | Diskutime | Muzik Shqip | Poezi | Lojra | Kontakt
1999 - 2014 Forumi Dardania
Te gjitha kohėt janė nė GMT +1. Ora tani ėshtė 05:26.
|
|

